Tema 14
Resolucion de problemas que implican el uso de ecuaciones cuadraticas. Aplicacion de la fórmula general para resolver dichas ecuaciones.
http://recursostic.educacion.es/descartes/web/Descartes1/4a_eso/Ecuacion_de_segundo_grado/Ecua_seg.htm
Son ecuaciones de segundo grado aquellas en las que la incógnita aparece al menos una vez elevada al cuadrado (x2 ). Por ejemplo: 3x2 - 3x = x - 1.
Pasemos al primer miembro de la ecuación todos los términos de forma que en el segundo miembro quede 0. Obtenemos:
3x2 - 4x + 1 = 0, que es la forma en que deberemos expresar todas la ecuaciones de segundo grado para resolverlas.
En muchos casos, una vez conseguida esta forma, la ecuación se puede simplificar, lo cual es muy conveniente. Por ejemplo:
Ejercicio 1.- Expresar en la forma más simple y simplificada posible, la ecuación:
3x2 - 3x/2 = x/2 - x + 2 + x2
Primero haremos denominador común para eliminar los denominadores existentes. Llegaremos a:
6x2 - 3x = x - 2x + 4 + 2x2
Expresando todos los términos en el primer miembro: 4x2 - 2x - 4 = 0
y simplificando (dividiendo todo por 2): : 2x2 - x - 2 = 0.
Los siguientes problemas se plantean mediante una ecuación de segundo grado, aunque luego al resolverla pueda dar lugar a una ecuación de primer grado en algún caso.
Problema 1.- Calcular la hipotenusa de un triángulo rectángulo, sabiendo que las medidas de sus lados son tres números consecutivos
Solución: Se puede realizar el siguiente dibujo del problema, teniendo en cuenta que la hipotenusa el el lado mayor y llamando "x" al menor de los catetos.
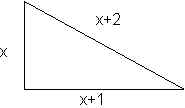Teniendo en cuenta el teorema de Pitágoras, se cumple: (x+2)2 = (x+ 1)2 + x2.
Operando: x2 + 4x + 4 = x 2 + 2x + 1+ x2.
Agrupando todos los términos en el segundo miembro y simplificando: x2 - 2x - 3 = 0
Ecuación que sabes resolver numéricamente, con soluciones: x = 3 y x = -1
Naturalmente la solución x =-1 hay que rechazarla porque un lado no puede tener una medida negativa, luego nos queda:
Hipotenusa: x + 2 = 5 ; Cateto mayor: x + 1 = 4 ; Cateto menor: x = 3.
Problema 2.- Un rectángulo la base mide el triple que la altura. Si disminuimos en 1 cm. cada lado, el área inicial disminuye en 15 cm . Calcular las dimensiones y el área del rectángulo inicial.
(Sugerencia: Realiza un dibujo del problema).
Solución: Base = 12 cm. Altura = 4 cm.
Problema 3.- Hallar tres números impares consecutivos, tales que si al cuadrado del mayor se le restan los cuadrados de los otros dos se obtiene como resultado 7.
(Solución: 5 , 7, y 9 )
Problema 4.- La edad de un padre es el cuadrado de la de su hijo. Dentro de 24 años la edad del padre será el doble de la del hijo. ¿Cuántos años tiene ahora cada uno?
(Solución: 6 y 36)
http://recursostic.educacion.es/descartes/web/Descartes1/4a_eso/Ecuacion_de_segundo_grado/Ecua_seg.htm
Son ecuaciones de segundo grado aquellas en las que la incógnita aparece al menos una vez elevada al cuadrado (x2 ). Por ejemplo: 3x2 - 3x = x - 1.
Pasemos al primer miembro de la ecuación todos los términos de forma que en el segundo miembro quede 0. Obtenemos:
3x2 - 4x + 1 = 0, que es la forma en que deberemos expresar todas la ecuaciones de segundo grado para resolverlas.
En muchos casos, una vez conseguida esta forma, la ecuación se puede simplificar, lo cual es muy conveniente. Por ejemplo:
Ejercicio 1.- Expresar en la forma más simple y simplificada posible, la ecuación:
3x2 - 3x/2 = x/2 - x + 2 + x2
Primero haremos denominador común para eliminar los denominadores existentes. Llegaremos a:
6x2 - 3x = x - 2x + 4 + 2x2
Expresando todos los términos en el primer miembro: 4x2 - 2x - 4 = 0
y simplificando (dividiendo todo por 2): : 2x2 - x - 2 = 0.
SOLUCIÓN GENERAL DE LA ECUACIÓN DE SEGUNDO GRADO
Como vimos en la descripción, cualquier ecuación de segundo grado se puede expresar de la forma:
ax2 +bx + c = 0
donde a, b y c serán números enteros (positivos o negativos). Para ello bastará obtener el denominador común (si hay denominadores), para eliminarlo y pasar todos los términos al primer miembro.
Sabemos que una vez conseguida dicha forma, las dos "posibles" soluciones de la ecuación son:
Así la ecuación del ejemplo inicial: 3x2 - 4x + 1 = 0: tendrá por soluciones: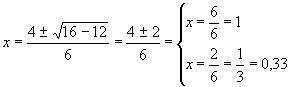
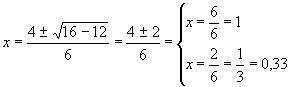
Luego 1 y 0,33 son las dos soluciones o raíces de la ecuación.
Ejercicio 2.- Resolver las siguientes ecuaciones
a) x2/2 = x/2 + 3
b) 3x2 = 12
Problema 1.- Calcular la hipotenusa de un triángulo rectángulo, sabiendo que las medidas de sus lados son tres números consecutivos
Solución: Se puede realizar el siguiente dibujo del problema, teniendo en cuenta que la hipotenusa el el lado mayor y llamando "x" al menor de los catetos.
Operando: x2 + 4x + 4 = x 2 + 2x + 1+ x2.
Agrupando todos los términos en el segundo miembro y simplificando: x2 - 2x - 3 = 0
Ecuación que sabes resolver numéricamente, con soluciones: x = 3 y x = -1
Naturalmente la solución x =-1 hay que rechazarla porque un lado no puede tener una medida negativa, luego nos queda:
Hipotenusa: x + 2 = 5 ; Cateto mayor: x + 1 = 4 ; Cateto menor: x = 3.
Problema 2.- Un rectángulo la base mide el triple que la altura. Si disminuimos en 1 cm. cada lado, el área inicial disminuye en 15 cm . Calcular las dimensiones y el área del rectángulo inicial.
(Sugerencia: Realiza un dibujo del problema).
Solución: Base = 12 cm. Altura = 4 cm.
Problema 3.- Hallar tres números impares consecutivos, tales que si al cuadrado del mayor se le restan los cuadrados de los otros dos se obtiene como resultado 7.
(Solución: 5 , 7, y 9 )
Problema 4.- La edad de un padre es el cuadrado de la de su hijo. Dentro de 24 años la edad del padre será el doble de la del hijo. ¿Cuántos años tiene ahora cada uno?
(Solución: 6 y 36)
Comentarios
Publicar un comentario